DIRICHLET (P. G. LEJEUNE-)

DIRICHLET (P. G. LEJEUNE-)

Avec son ami et contemporain Jacobi et son cadet de quelques années Kummer, Dirichlet constitue la première génération des mathématiciens allemands après Gauss, dont naturellement ils subissent très fortement l’influence; mais, alors que celui-ci était resté très à l’écart et n’avait pratiquement pas eu d’élèves, ce sont eux qui fondent véritablement la grande école allemande du XIX^e et du XX^e siècle.

Les travaux de Dirichlet en analyse et dans les applications de cette dernière à la mécanique ou à la physique mathématique témoignent d’une grande virtuosité de calcul, mais à laquelle s’allient un sens aigu de la rigueur et un penchant tout moderne pour les preuves «conceptuelles» débarrassées de calculs parasites.

Mais le sujet de prédilection de Dirichlet, pendant toute sa carrière, a été la théorie des nombres, où il a fait ses plus belles découvertes. On lui doit deux outils puissants: le célèbre principe des tiroirs et les séries de Dirichlet dont il sut montrer toute la fécondité.

Travaux d’analyse

Dirichlet est beaucoup plus soigneux et rigoureux que Cauchy lui-même, et ses démonstrations de convergence (les premières en date) des développements en série de Fourier ou en série de polynômes de Legendre sont restées des modèles à cet égard.

Dans une étude de quelques pages sur le potentiel, il introduit l’intégrale de Dirichlet:

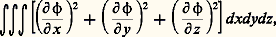pour prouver l’unicité de la distribution de masses ayant un potentiel donné, inaugurant ainsi ce que, depuis Riemann, on appelle encore aujourd’hui le problème de Dirichlet pour les équations aux dérivées partielles elliptiques et leur généralisations.

En mécanique, enfin, on ne peut omettre de mentionner sa célèbre démonstration en quelques lignes de la condition classique d’équilibre d’un système matériel, là où ses prédécesseurs se perdaient en considérations peu probantes fondées sur des développements en série plus ou moins valables.

Théorie des nombres

Dirichlet était un des rares mathématiciens de sa génération à connaître à fond les Disquisitiones arithmeticae de Gauss qui ne quittaient jamais sa table de travail et où il a puisé mainte inspiration: il est très souvent revenu aux problèmes de la théorie des formes quadratiques binaires et ternaires, et a généralisé cette théorie aux formes sur l’anneau des entiers de Gauss; il a donné d’ingénieuses méthodes pour démontrer les évaluations asymptotiques de diverses fonctions arithmétiques (par exemple la moyenne du nombre de diviseurs des n premiers nombres entiers) indiquées sans démonstration par Gauss; et parmi ses premiers travaux (publiés dès sa vingt et unième année) figure une démonstration de l’impossibilité en nombres entiers de l’équation x ⁵ + y ⁵ = z ⁵.

Ses travaux les plus importants dans la théorie des nombres reposent sur deux principes nouveaux, qui sont demeurés jusqu’à nos jours d’une extraordinaire fécondité. Le premier est d’une simplicité déconcertante; c’est le principe des tiroirs, d’après lequel si n + 1 objets sont arbitrairement répartis dans n casiers, il y aura toujours un de ces derniers qui contiendra deux objets au moins. Si banale que puisse sembler cette remarque, il est merveilleux de voir ce qu’en tire Dirichlet. Par exemple, soit un nombre irrationnel, et soit q un entier 礪 0; divisons l’intervalle 0 諒 t 諒 1 en q parties égales, et considérons les parties fractionnaires des multiples p de pour 0 諒 p 諒 q (c’est-à-dire la différence entre p et le plus grand entier qui lui est inférieur). Aucun des nombres p n’est entier, et toutes les parties fractionnaires des p sont distinctes, puisque est irrationnel. Donc, parmi ces q + 1 nombres, il y en a deux au moins qui appartiennent à l’un des q intervalles en lesquels nous avons subdivisé l’intervalle 0 諒 t 諒 1. Autrement dit, on a, pour un entier k tel que 0 諒 k 諒 q 漣 1:

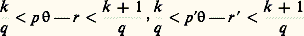pour deux entiers p , p tels que 0 諒 p 諒 q , 0 諒 p 諒 q , r et r étant deux entiers. En retranchant, on obtient:

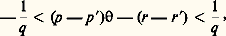et comme p p , on a prouvé l’existence d’un entier h tel que 1 諒 h 諒 q , vérifiant la relation |h 漣 s | 麗 1/q pour un entier s convenable. On ne savait avant Dirichlet prouver ce théorème que par des considérations assez compliquées sur les fractions continuées (cf. approximations DIOPHANTIENNES). Grâce à cette méthode, appliquée avec une très grande ingéniosité, Dirichlet put faire progresser considérablement la théorie des entiers d’un corps de nombres algébriques en déterminant dans le cas le plus général la structure du groupe des unités de ce corps (c’est-à-dire les entiers du corps dont l’inverse est aussi un entier).

Séries de Dirichlet

Le second principe introduit par Dirichlet est l’usage des séries qui portent son nom, par où il inaugurait la théorie analytique des nombres. Dirichlet part d’une remarque d’Euler, qui avait établi l’identité:

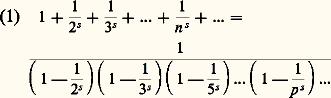(s 礪 1), où le produit du second membre est étendu à tous les nombres premiers, et avait conclu du fait que la série du premier membre diverge pour s = 1 une nouvelle démonstration du fait qu’il y a une infinité de nombres premiers. La méthode imaginée par Dirichlet a pour objet de prouver la même conclusion pour ceux des nombres premiers qui appartiennent à une progression arithmétique donnée an + b (a et b entiers premiers entre eux), par l’examen du comportement d’une série analogue au premier membre de (1) lorsque s tend vers 1; il n’est pas possible de donner ici plus de détails sur cette technique raffinée, sans commune mesure avec la remarque élémentaire d’Euler, et où s’allient subtilement une aussi grande maîtrise dans le maniement de l’analyse que dans la connaissance approfondie des lois de la théorie des nombres. Un peu plus tard, en comparant par deux procédés (l’un utilisant l’analyse, l’autre la théorie des formes quadratiques) le comportement au voisinage de s = 1 d’une autre série de Dirichlet, il obtenait, pour le nombre des classes des formes quadratiques binaires de discriminant donné, des expressions remarquables que ses prédécesseurs Gauss et Jacobi n’avaient su démontrer que dans des cas particuliers. Plus tard, Kummer, pour les corps de racines de l’unité, et Dedekind, dans le cas général, devaient montrer que la méthode de Dirichlet s’adapte à tous les cas et donne une méthode de calcul direct du nombre de classes d’idéaux d’un corps de nombres algébriques.

Encyclopédie Universelle. 2012.